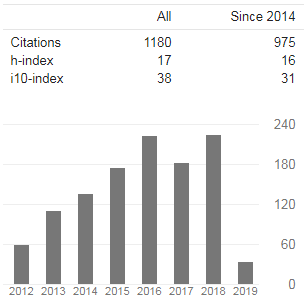
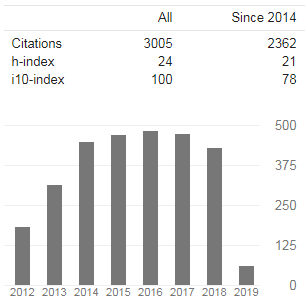
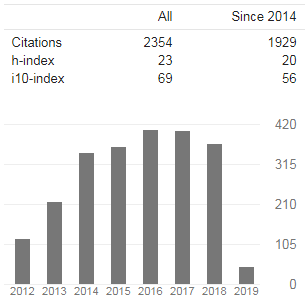
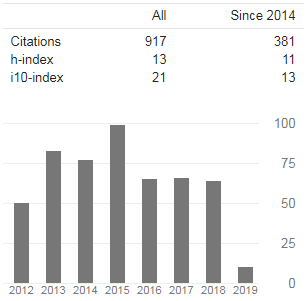
The International Journals of Engineering and Sciences (IJENS) visualize to prosper across the continents by providing a magnificent platform to publish the research papers of excellent theoretical and applied research in all present and future era Engineering, Computing and Sciences regulations. From basic research to application development in all the fields of studies of below mentioned regulations is the broad range of IJENS. The International Journals of Engineering and Sciences are excellent, intellectual, peer reviewed combination of journals that take a scholarly approach in creating, developing, integrating, sharing and applying knowledge about all the fields of study in Engineering, Computing and Sciences for the benefit of humanity and the profession. It provides rapid publications and a forum to the academics, scholars and advanced level students for exchanging significant information and productive ideas associated with all these disciplines. Papers published in IJENS take an intellectual approach to knowledge, wisdom, training and learning. They establish a clear connection to student learning, and appeal to a wide range of audience interested in Engineering, Computing education and Sciences. The teachers, researchers, instructors, curriculum designers, and administrators are the key beneficial of IJENS.

IJMME: International Journal of Mechanical and Mechatronics Engineering
ISSN: 2077-124X (Online) 2227-2771 (Print) Impact Factor: 1.201
Publication Frequency - Bi-Monthly
Publisher - IJENS Publisher, Rawalpindi, Pakistan
Home Page | Call for Paper | Editorial Board |Archive | Citations

IJET: International Journal of Engineering and Technology
ISSN: 2077-1185 (Online) 2227-2712 (Print) Impact Factor: 1.272
Publication Frequency - Bi-Monthly
Publisher - IJENS Publisher, Rawalpindi, Pakistan
Home Page | Call for Paper | Editorial Board |Archive | Citations

IJBAS: International Journal of Basic and Applied Sciences
ISSN: 2077-1223 (Online) 2227-2720 (Print) Impact Factor: 1.220
Publication Frequency - Bi-Monthly
Publisher - IJENS Publisher, Rawalpindi, Pakistan
Home Page | Call for Paper | Editorial Board | Archive | Citations

IJECS: International Journal of Electrical and Computer Sciences
ISSN: 2077-1231 (Online) 2227-2739 (Print) Impact Factor: 1.428
Publication Frequency - Bi-Monthly
Publisher - IJENS Publisher, Rawalpindi, Pakistan
Home Page | Call for Paper | Editorial Board |Archive | Citations

IJVIPNS: International Journal of Video and Image Processing and Network Security
ISSN: 2077-1207 (Online) 2227-2755 (Print) Impact Factor: 2.406
Publication Frequency - Bi-Monthly
Publisher - IJENS Publisher, Rawalpindi, Pakistan
Home Page | Call for Paper | Editorial Board |Archive | Citations

IJCEE: International Journal of Civil and Environmental Engineering
ISSN: 2077-1258 (Online) 2227-2763 (Print) Impact Factor: 1.299
Publication Frequency - Bi-Monthly
Publisher - IJENS Publisher, Rawalpindi, Pakistan
Home Page | Call for Paper | Editorial Board |Archive | Citations